File:An infinitely differentiable function which is not analytic illustration.png
From Wikimedia Commons, the free media repository
Jump to navigation
Jump to search
An_infinitely_differentiable_function_which_is_not_analytic_illustration.png (500 × 146 pixels, file size: 6 KB, MIME type: image/png)
File information
Structured data
Captions
Captions
Add a one-line explanation of what this file represents
Summary
[edit]
|
File:Expinvsq5.svg is a vector version of this file. It should be used in place of this PNG file when not inferior.
File:An infinitely differentiable function which is not analytic illustration.png → File:Expinvsq5.svg
For more information, see Help:SVG.
|
Transferred from en.wikipedia to Commons by Maksim.
The original description page was here. All following user names refer to en.wikipedia.
This diagram was created with MATLAB.
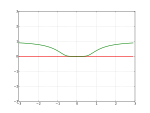
| DescriptionAn infinitely differentiable function which is not analytic illustration.png | An infinitely differentiable function which is not analytic illustration | |||
| Date | ||||
| Source | Own work | |||
| Author | Mathbot | |||
| Permission (Reusing this file) |
|
|||
| Source code InfoField | MATLAB codefunction main()
thickness1=2; thickness2=1.5; arrowsize=10; arrow_type=2; ball_rad=0.03;
blue=[0, 0, 1]; black=[0 0 0]; fontsize=floor(20); dist=0.01;
a=-4; b=4;
h=0.01;
X=a:h:b;
Y=zeros(length(X), 1);
for i=1:length(X)
x=X(i);
if x == 0 Y(i)=0;
else
Y(i)=exp(-1/x^2);
end
end
figure(1); clf; hold on; axis equal; axis off
arrow([a 0], [b+0.2, 0], thickness2, arrowsize, pi/8,arrow_type, [0, 0, 0])
arrow([0 -0.3], [0 2.*max(Y)], thickness2, arrowsize, pi/8,arrow_type, [0, 0, 0])
plot(X, Y, 'linewidth', thickness1, 'color', blue);
plot(X, 0*Y+1, 'linewidth', thickness2/1.5, 'color', black, 'linestyle', '--');
arrow([b+0.1 0], [b+0.2, 0], thickness2, arrowsize, pi/8,arrow_type, [0, 0, 0])
ball(0, 0, ball_rad, blue); place_text_smartly(0, fontsize, 5, dist, '0');
ball(0, 1, ball_rad, black); place_text_smartly(sqrt(-1), fontsize, 5, dist, '1');
saveas(gcf, 'An_infinitely_differentiable_function_which_is_not_analytic_illustration.eps', 'psc2')
function place_text_smartly (z, fs, pos, d, tx)
p=cos(pi/4)+sqrt(-1)*sin(pi/4);
z = z + p^pos * d * fs;
shiftx=0.0003;
shifty=0.002;
x = real (z); y=imag(z);
H=text(x+shiftx*fs, y+shifty*fs, tx); set(H, 'fontsize', fs, 'HorizontalAlignment', 'c', 'VerticalAlignment', 'c')
function ball(x, y, r, color)
Theta=0:0.1:2*pi;
X=r*cos(Theta)+x;
Y=r*sin(Theta)+y;
H=fill(X, Y, color);
set(H, 'EdgeColor', color);
function arrow(start, stop, thickness, arrowsize, sharpness, arrow_type, color)
% draw a line with an arrow at the end
% start is the x,y point where the line starts
% stop is the x,y point where the line stops
% thickness is an optional parameter giving the thickness of the lines
% arrowsize is an optional argument that will give the size of the arrow
% It is assumed that the axis limits are already set
% 0 < sharpness < pi/4 determines how sharp to make the arrow
% arrow_type draws the arrow in different styles. Values are 0, 1, 2, 3.
% 8/4/93 Jeffery Faneuff
% Copyright (c) 1988-93 by the MathWorks, Inc.
% Modified by Oleg Alexandrov 2/16/03
if nargin <=6
color=[0, 0, 0];
end
if (nargin <=5)
arrow_type=0; % the default arrow, it looks like this: ->
end
if (nargin <=4)
sharpness=pi/4; % the arrow sharpness - default = pi/4
end
if nargin<=3
xl = get(gca,'xlim');
yl = get(gca,'ylim');
xd = xl(2)-xl(1);
yd = yl(2)-yl(1);
arrowsize = (xd + yd) / 2; % this sets the default arrow size
end
if (nargin<=2)
thickness=0.5; % default thickness
end
xdif = stop(1) - start(1);
ydif = stop(2) - start(2);
if (xdif == 0)
if (ydif >0)
theta=pi/2;
else
theta=-pi/2;
end
else
theta = atan(ydif/xdif); % the angle has to point according to the slope
end
if(xdif>=0)
arrowsize = -arrowsize;
end
if (arrow_type == 0) % draw the arrow like two sticks originating from its vertex
xx = [start(1), stop(1),(stop(1)+0.02*arrowsize*cos(theta+sharpness)),NaN,stop(1),...
(stop(1)+0.02*arrowsize*cos(theta-sharpness))];
yy = [start(2), stop(2), (stop(2)+0.02*arrowsize*sin(theta+sharpness)),NaN,stop(2),...
(stop(2)+0.02*arrowsize*sin(theta-sharpness))];
plot(xx,yy, 'LineWidth', thickness, 'color', color)
end
if (arrow_type == 1) % draw the arrow like an empty triangle
xx = [stop(1),(stop(1)+0.02*arrowsize*cos(theta+sharpness)), ...
stop(1)+0.02*arrowsize*cos(theta-sharpness)];
xx=[xx xx(1) xx(2)];
yy = [stop(2),(stop(2)+0.02*arrowsize*sin(theta+sharpness)), ...
stop(2)+0.02*arrowsize*sin(theta-sharpness)];
yy=[yy yy(1) yy(2)];
plot(xx,yy, 'LineWidth', thickness, 'color', color)
% plot the arrow stick
plot([start(1) stop(1)+0.02*arrowsize*cos(theta)*cos(sharpness)], [start(2), stop(2)+ ...
0.02*arrowsize*sin(theta)*cos(sharpness)], 'LineWidth', thickness, 'color', color)
end
if (arrow_type==2) % draw the arrow like a full triangle
xx = [stop(1),(stop(1)+0.02*arrowsize*cos(theta+sharpness)), ...
stop(1)+0.02*arrowsize*cos(theta-sharpness),stop(1)];
yy = [stop(2),(stop(2)+0.02*arrowsize*sin(theta+sharpness)), ...
stop(2)+0.02*arrowsize*sin(theta-sharpness),stop(2)];
% plot the arrow stick
plot([start(1) stop(1)+0.01*arrowsize*cos(theta)], [start(2), stop(2)+ ...
0.01*arrowsize*sin(theta)], 'LineWidth', thickness, 'color', color)
H=fill(xx, yy, color);% fill with black
set(H, 'EdgeColor', 'none')
end
if (arrow_type==3) % draw the arrow like a filled 'curvilinear' triangle
curvature=0.5; % change here to make the curved part more curved (or less curved)
radius=0.02*arrowsize*max(curvature, tan(sharpness));
x1=stop(1)+0.02*arrowsize*cos(theta+sharpness);
y1=stop(2)+0.02*arrowsize*sin(theta+sharpness);
x2=stop(1)+0.02*arrowsize*cos(theta)*cos(sharpness);
y2=stop(2)+0.02*arrowsize*sin(theta)*cos(sharpness);
d1=sqrt((x1-x2)^2+(y1-y2)^2);
d2=sqrt(radius^2-d1^2);
d3=sqrt((stop(1)-x2)^2+(stop(2)-y2)^2);
center(1)=stop(1)+(d2+d3)*cos(theta);
center(2)=stop(2)+(d2+d3)*sin(theta);
alpha=atan(d1/d2);
Alpha=-alpha:0.05:alpha;
xx=center(1)-radius*cos(Alpha+theta);
yy=center(2)-radius*sin(Alpha+theta);
xx=[xx stop(1) xx(1)];
yy=[yy stop(2) yy(1)];
% plot the arrow stick
plot([start(1) center(1)-radius*cos(theta)], [start(2), center(2)- ...
radius*sin(theta)], 'LineWidth', thickness, 'color', color);
H=fill(xx, yy, color);% fill with black
set(H, 'EdgeColor', 'none')
end
|
| date/time | username | edit summary |
|---|---|---|
| 04:41, 23 November 2005 | en:User:Oleg Alexandrov | (fix bug) |
| 04:34, 23 November 2005 | en:User:Oleg Alexandrov | (<span class="autocomment"><a href="/wiki/Image:An_infinitely_differentiable_function_which_is_not_analytic_illustration.png#Source_code" title="Image:An infinitely differentiable function which is not analytic illustration.png">→</a>Source code -</span> lang) |
| 04:33, 23 November 2005 | en:User:Mathbot | (source_code) |
| 04:32, 23 November 2005 | en:User:Oleg Alexandrov | (format) |
| 04:29, 23 November 2005 | en:User:Oleg Alexandrov |
Licensing
[edit]| Public domainPublic domainfalsefalse |
| I, the copyright holder of this work, release this work into the public domain. This applies worldwide. In some countries this may not be legally possible; if so: I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law. |
Original upload log
[edit]Legend: (cur) = this is the current file, (del) = delete this old version, (rev) = revert to this old version.
Click on date to download the file or see the image uploaded on that date.
- (del) (cur) 04:43, 23 November 2005 . . en:User:Oleg_Alexandrov Oleg Alexandrov ( en:User_talk:Oleg_Alexandrov Talk) . . 500x146 (6584 bytes)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 16:47, 18 March 2006 | 500 × 146 (6 KB) | Maksim (talk | contribs) | La bildo estas kopiita de wikipedia:en. La originala priskribo estas: == Licensing == {{PD-self}} ==Source code (Matlab)== <pre> <nowiki> function main() thickness1=2; thickness2=1.5; arrowsize=10; arrow_type=2; ball_rad=0.03; blue=[0, 0, 1]; |
You cannot overwrite this file.
File usage on Commons
There are no pages that use this file.
File usage on other wikis
The following other wikis use this file:
- Usage on fr.wikiversity.org