File:Gradient descent.png
From Wikimedia Commons, the free media repository
Jump to navigation
Jump to search
Gradient_descent.png (482 × 529 pixels, file size: 25 KB, MIME type: image/png)
File information
Structured data
Captions
Captions
Add a one-line explanation of what this file represents
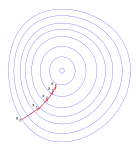
Иллюстрация градиентного спуска
Summary
[edit]
|
File:Gradient descent.svg is a vector version of this file. It should be used in place of this PNG file when not inferior.
File:Gradient descent.png → File:Gradient descent.svg
For more information, see Help:SVG.
|
| DescriptionGradient descent.png | An illustration of the gradient descent method. I graphed this with Matlab |
| Date | 19 November 2004 (original upload date) |
| Source | Transferred from en.wikipedia to Commons. |
| Author | Olegalexandrov at English Wikipedia |
This diagram was created with MATLAB.
Moved from en:Wikipedia, converted to png, and added the matlab source code. Oleg Alexandrov 03:33, 23 June 2007 (UTC)
Licensing
[edit]| Public domainPublic domainfalsefalse |
| I, the copyright holder of this work, release this work into the public domain. This applies worldwide. In some countries this may not be legally possible; if so: I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law. |
% Illustration of gradient descent
function main()
% the ploting window
figure(1);
clf; hold on;
set(gcf, 'color', 'white');
set(gcf, 'InvertHardCopy', 'off');
axis equal; axis off;
% the box
Lx1=-2; Lx2=2; Ly1=-2; Ly2=2;
% the function whose contours will be plotted
N=60; h=1/N;
XX=Lx1:h:Lx2;
YY=Ly1:h:Ly2;
[X, Y]=meshgrid(XX, YY);
f=inline('-((y+1).^4/25+(x-1).^4/10+x.^2+y.^2-1)');
Z=f(X, Y);
% the contours
h=0.3; l0=-1; l1=20;
l0=h*floor(l0/h);
l1=h*floor(l1/h);
v=[l0:1.5*h:0 0:h:l1 0.8 0.888];
[c,h] = contour(X, Y, Z, v, 'b');
% graphing settings
small=0.08;
small_rad = 0.01;
thickness=1; arrowsize=0.06; arrow_type=2;
fontsize=13;
red = [1, 0, 0];
white = 0.99*[1, 1, 1];
% initial guess for gradient descent
x=-0.6498; y=-1.0212;
% run several iterations of gradient descent
for i=0:4
H=text(x-1.5*small, y+small/2, sprintf('x_%d', i));
set(H, 'fontsize', fontsize, 'color', 0*[1 1 1]);
% the derivatives in x and in y, the step size
u=-2/5*(x-1)^3-2*x;
v=-4/25*(y+1)^3-2*y;
alpha=0.11;
if i< 4
plot([x, x+alpha*u], [y, y+alpha*v]);
arrow([x, y], [x, y]+alpha*[u, v], thickness, arrowsize, pi/8, ...
arrow_type, [1, 0, 0])
x=x+alpha*u; y=y+alpha*v;
end
end
% some dummy text, to expand the saving window a bit
text(-0.9721, -1.5101, '*', 'color', white);
text(1.5235, 1.1824, '*', 'color', white);
% save to eps
saveas(gcf, 'Gradient_descent.eps', 'psc2')
function arrow(start, stop, thickness, arrow_size, sharpness, arrow_type, color)
% Function arguments:
% start, stop: start and end coordinates of arrow, vectors of size 2
% thickness: thickness of arrow stick
% arrow_size: the size of the two sides of the angle in this picture ->
% sharpness: angle between the arrow stick and arrow side, in radians
% arrow_type: 1 for filled arrow, otherwise the arrow will be just two segments
% color: arrow color, a vector of length three with values in [0, 1]
% convert to complex numbers
i=sqrt(-1);
start=start(1)+i*start(2); stop=stop(1)+i*stop(2);
rotate_angle=exp(i*sharpness);
% points making up the arrow tip (besides the "stop" point)
point1 = stop - (arrow_size*rotate_angle)*(stop-start)/abs(stop-start);
point2 = stop - (arrow_size/rotate_angle)*(stop-start)/abs(stop-start);
if arrow_type==1 % filled arrow
% plot the stick, but not till the end, looks bad
t=0.5*arrow_size*cos(sharpness)/abs(stop-start); stop1=t*start+(1-t)*stop;
plot(real([start, stop1]), imag([start, stop1]), 'LineWidth', thickness, 'Color', color);
% fill the arrow
H=fill(real([stop, point1, point2]), imag([stop, point1, point2]), color);
set(H, 'EdgeColor', 'none')
else % two-segment arrow
plot(real([start, stop]), imag([start, stop]), 'LineWidth', thickness, 'Color', color);
plot(real([stop, point1]), imag([stop, point1]), 'LineWidth', thickness, 'Color', color);
plot(real([stop, point2]), imag([stop, point2]), 'LineWidth', thickness, 'Color', color);
end
function ball(x, y, r, color)
Theta=0:0.1:2*pi;
X=r*cos(Theta)+x;
Y=r*sin(Theta)+y;
H=fill(X, Y, color);
set(H, 'EdgeColor', 'none');
Original upload log
[edit]The original description page was here. All following user names refer to en.wikipedia.
- 2004-11-19 02:41 Olegalexandrov 471×492×8 (27067 bytes) An illustration of the gradient descent method. I graphed this with Matlab {{PD}}
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 03:33, 23 June 2007 |  | 482 × 529 (25 KB) | Oleg Alexandrov (talk | contribs) | {{Information |Description=An illustration of the gradient descent method. I graphed this with Matlab |Source=Originally from [http://en.wikipedia.org en.wikipedia]; description page is/was [http://en.wikipedia.org/w/index.php?title=Image%3AGradient_desce |
You cannot overwrite this file.
File usage on Commons
The following 2 pages use this file:
File usage on other wikis
The following other wikis use this file:
- Usage on en.wikipedia.org
- Usage on et.wikipedia.org
- Usage on fa.wikipedia.org
- Usage on fr.wikipedia.org
- Usage on gl.wikipedia.org
- Usage on ko.wikipedia.org
- Usage on lt.wikipedia.org
- Usage on pl.wikipedia.org
- Usage on pt.wikipedia.org
- Usage on ru.wikipedia.org
- Usage on sv.wikipedia.org
- Usage on zh.wikipedia.org