File:Partial transmittance.gif
From Wikimedia Commons, the free media repository
Jump to navigation
Jump to search
Partial_transmittance.gif (367 × 161 pixels, file size: 67 KB, MIME type: image/gif, looped, 53 frames, 4.2 s)
File information
Structured data
Captions
Captions
Add a one-line explanation of what this file represents
Summary
[edit]| DescriptionPartial transmittance.gif |
Русский: Показано классическое отражение/прохождение солитона гауссового импульса от/в более плотную среду. В реальности же, свет отражается не от поверхности, а от всех частиц тела (см. ru:КЭД). English: Illustration of partial reflection of a wave. A gaussian wave on a one-dimensional string strikes a boundary with transmission coefficient of 0.5. Half the wave is transmitted and half is reflected.
Français : Illustration de la réflection partielle d'une onde. Une onde gaussienne se déplaçant sur un ressort unidimensionnel est réfléchie/transmise au niveau d'une interface avec un coefficient de transmission de 0.5.
Español: Ilustración de una reflexión parcial de una onda. Una onda gaussiana sobre una cuerda de una dimensión choca contra un limite con un coeficiente de transmisión de 0.5. La mitad de la onda es transmitida y la otra mitad es reflejada. |
| Date | |
| Source | self-made with MATLAB, source code below |
| Author | Oleg Alexandrov |
This diagram was created with MATLAB.
Licensing
[edit]| Public domainPublic domainfalsefalse |
| I, the copyright holder of this work, release this work into the public domain. This applies worldwide. In some countries this may not be legally possible; if so: I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law. |
MATLAB source code
[edit]% Partial transmittance and reflectance of a wave
% Code is messed up, don't have time to clean it now
function main()
% KSmrq's colors
red = [0.867 0.06 0.14];
blue = [0, 129, 205]/256;
green = [0, 200, 70]/256;
yellow = [254, 194, 0]/256;
white = 0.99*[1, 1, 1];
black = [0, 0, 0];
% length of the string and the grid
L = 5;
N = 151;
X=linspace(0, L, N);
h = X(2)-X(1); % space grid size
c = 0.01; % speed of the wave
tau = 0.25*h/c; % time grid size
% form a medium with a discontinuous wave speed
C = 0*X+c;
D=L/2;
c_right = 0.5*c; % speed to the right of the disc
for i=1:N
if X(i) > D
C(i) = c_right;
end
end
% Now C = c for x < D, and C=c_right for x > D
K = 5; % steepness of the bump
S = 0; % shift the wave
f=inline('exp(-K*(x-S).^2)', 'x', 'S', 'K'); % a gaussian as an initial wave
df=inline('-2*K*(x-S).*exp(-K*(x-S).^2)', 'x', 'S', 'K'); % derivative of f
% wave at time 0 and tau
U0 = 0*f(X, S, K);
U1 = U0 - 2*tau*c*df(X, S, K);
U = 0*U0; % current U
% plot between Start and End
Start=130; End=500;
% hack to capture the first period of the wave
min_k = 2*N; k_old = min_k; turn_on = 0;
frame_no = 0;
for j=1:End
% fixed end points
U(1)=0; U(N)=0;
% finite difference discretization in time
for i=2:(N-1)
U(i) = (C(i)*tau/h)^2*(U1(i+1)-2*U1(i)+U1(i-1)) + 2*U1(i) - U0(i);
end
% update info, for the next iteration
U0 = U1; U1 = U;
spacing=7;
% plot the wave
if rem(j, spacing) == 1 & j > Start
figure(1); clf; hold on;
axis equal; axis off;
lw = 3; % linewidth
% size of the window
ys = 1.2;
low = -0.5*ys;
high = ys;
plot([D, D], [low, high], 'color', black, 'linewidth', 0.7*lw)
% fill([X(1), D, D, X(1)], [low, low, high, high], [0.9, 1, 1], 'edgealpha', 0);
% fill([D X(N), X(N), D], [low, low, high, high], [1, 1, 1], 'edgealpha', 0);
plot(X, U, 'color', red, 'linewidth', lw);
% plot the ends of the string
small_rad = 0.06;
axis([-small_rad, 0.82*L, -ys, ys]);
% small markers to keep the bounding box fixed when saving to eps
plot(-small_rad, ys, '*', 'color', white);
plot(L+small_rad, -ys, '*', 'color', white);
pause(0.1)
frame_no = frame_no + 1;
%frame=sprintf('Frame%d.eps', 1000+frame_no); saveas(gcf, frame, 'psc2');
frame=sprintf('Frame%d.png', 1000+frame_no);% saveas(gcf, frame);
disp(frame)
print (frame, '-dpng', '-r300');
end
end
% The gif image was creating with the command
% convert -antialias -loop 10000 -delay 8 -compress LZW -scale 20% Frame10*png Partial_transmittance.gif
% and was later cropped in Gimp
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 16:36, 9 April 2010 |  | 367 × 161 (67 KB) | Aiyizo (talk | contribs) | optimized animation |
| 05:56, 26 November 2007 | 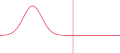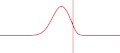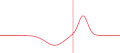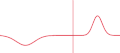 | 367 × 161 (86 KB) | Oleg Alexandrov (talk | contribs) | {{Information |Description=Illustration of en:Transmission coefficient (optics) |Source=self-made with MATLAB, source code below |Date=~~~~~ |Author= Oleg Alexandrov |Permission=PD-self, see below |other_versions= }} {{PD-se |
You cannot overwrite this file.
File usage on Commons
The following page uses this file:
File usage on other wikis
The following other wikis use this file:
- Usage on ar.wikipedia.org
- Usage on bg.wikipedia.org
- Usage on ca.wikipedia.org
- Usage on de.wikipedia.org
- Reflexion (Physik)
- Fresnelsche Formeln
- Zeitbereichsreflektometrie
- Anpassungsdämpfung
- Benutzer Diskussion:Bleckneuhaus
- Wikipedia Diskussion:WikiProjekt SVG/Archiv/2012
- Wellenwiderstand
- Benutzer:Ariser/Stehwellenverhältnis Alternativentwurf
- Benutzer:Herbertweidner/Stehwellenverhältnis Alternativentwurf
- Benutzer:Physikaficionado/Fresnelsche Formeln-Röntgenstrahlung
- Usage on de.wikibooks.org
- Usage on en.wikipedia.org
- Usage on en.wikibooks.org
- Usage on en.wikiversity.org
- Quantum mechanics/Timeline
- How things work college course/Quantum mechanics timeline
- Quantum mechanics/Wave equations in quantum mechanics
- MATLAB essential/General information + arrays and matrices
- WikiJournal of Science/Submissions/Introduction to quantum mechanics
- WikiJournal of Science/Issues/0
- Talk:A card game for Bell's theorem and its loopholes/Conceptual
- Wright State University Lake Campus/2019-1/Broomstick
- Physics for beginners
- MyOpenMath/Physics images
- Usage on es.wikipedia.org
- Usage on et.wikipedia.org
- Usage on fa.wikipedia.org
- Usage on fa.wikibooks.org
- Usage on fr.wikipedia.org
- Usage on he.wikipedia.org
- Usage on hy.wikipedia.org
View more global usage of this file.
