File:Two-representations-of-L6n1-link-as-linked-circles.svg

From Wikimedia Commons, the free media repository
Jump to navigation Jump to search

Original file (SVG file, nominally 800 × 385 pixels, file size: 8 KB)

Captions

Captions

Add a one-line explanation of what this file represents
Description Two topologically-equivalent representations of the L6n1 or (3,3) torus link of mathematical knot theory, in the form of linked rings (see http://www.liv.ac.uk/~spmr02/rings/types.html ). One configuration has 3-fold rotational symmetry, the other doesn't. Neither of them is the Borromean rings.
Date
Source

Self-made graphic, converted from a version of the following vector PostScript source code: 

%!
300 282 translate/plr{dup 3 2 roll 72 mul 90 add dup 3 1
roll cos mul 3 1 roll sin mul}def 23.1130905 setlinewidth
/A{0.5 4 4.5{100 plr 78 0 360 arc closepath stroke}for 0
182 plr 78 0 360 arc closepath stroke}def A 11.5565453
setlinewidth 1 setgray A showpage
%EOF
Author AnonMoos
Permission
(Reusing this file)
Public domain I, the copyright holder of this work, release this work into the public domain. This applies worldwide.
In some countries this may not be legally possible; if so:
I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current13:29, 5 July 2011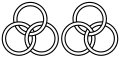Thumbnail for version as of 13:29, 5 July 2011800 × 385 (8 KB)AnonMoos (talk | contribs)streamline SVG
13:03, 5 July 2011Thumbnail for version as of 13:03, 5 July 2011800 × 385 (10 KB)AnonMoos (talk | contribs)Two topologically-equivalent representations of the [http://katlas.math.toronto.edu/wiki/L6n1 L6n1] or (3,3) torus link of mathematical knot theory, in the form of linked rings. One configuration has 3-fold rotational symmetry, the other doesn't. Neithe

You cannot overwrite this file.

Metadata

This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.

Retrieved from "https://commons.wikimedia.org/w/index.php?title=File:Two-representations-of-L6n1-link-as-linked-circles.svg&oldid=788924865"