File:VFPt metal balls largesmall.svg

Original file (SVG file, nominally 800 × 600 pixels, file size: 46 KB)
Captions
Captions
Summary
[edit]| DescriptionVFPt metal balls largesmall.svg |
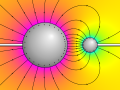
English: Electric field around a large and a small conducting sphere at opposite electric potential. The shape of the field lines is computed exactly, using the method of image charges with an infinite series of charges inside the two spheres. Field lines are always orthogonal to the surface of each sphere. In reality, the field is created by a continuous charge distribution at the surface of each sphere, indicated by small plus and minus signs. |
||
| Date | |||
| Source | Own work | ||
| Author | Geek3 | ||
| Other versions |
|
||
| SVG development InfoField | This W3C-invalid vector image was created with Inkscape, or with something else.
| ||
| Source code InfoField | SVG code# paste this code at the end of VectorFieldPlot 1.10
# https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot
u = 100.0
doc = FieldplotDocument('VFPt_metal_balls_largesmall',
commons=True, width=800, height=600, center=[400, 300], unit=u)
# define two spheres with position, radius and charge
s1 = {'p':sc.array([-1.0, 0.]), 'r':1.5}
s2 = {'p':sc.array([2.0, 0.]), 'r':0.5}
# make charge proportional to capacitance, which is proportional to radius.
s1['q'] = s1['r']
s2['q'] = -s2['r']
d = vabs(s2['p'] - s1['p'])
v12 = (s2['p'] - s1['p']) / d
# compute series of charges https://dx.doi.org/10.2174/1874183500902010032
charges = [[s1['p'][0], s1['p'][1], s1['q']], [s2['p'][0], s2['p'][1], s2['q']]]
r1 = r2 = 0.
q1, q2 = s1['q'], s2['q']
q0 = max(fabs(q1), fabs(q2))
for i in range(10):
q1, q2 = -s1['r'] * q2 / (d - r2), -s2['r'] * q1 / (d - r1),
r1, r2 = s1['r']**2 / (d - r2), s2['r']**2 / (d - r1)
p1, p2 = s1['p'] + r1 * v12, s2['p'] - r2 * v12
charges.append([p1[0], p1[1], q1])
charges.append([p2[0], p2[1], q2])
if max(fabs(q1), fabs(q2)) < 1e-3 * q0:
break
field = Field({'monopoles':charges})
# draw symbols
for c in charges:
doc.draw_charges(Field({'monopoles':[c]}), scale=0.6*sqrt(fabs(c[2])))
gradr = doc.draw_object('linearGradient', {'id':'rod_shade', 'x1':0, 'x2':0,
'y1':0, 'y2':1, 'gradientUnits':'objectBoundingBox'}, group=doc.defs)
for col, of in (('#666', 0), ('#ddd', 0.6), ('#fff', 0.7), ('#ccc', 0.75),
('#888', 1)):
doc.draw_object('stop', {'offset':of, 'stop-color':col}, group=gradr)
gradb = doc.draw_object('radialGradient', {'id':'metal_spot', 'cx':'0.53',
'cy':'0.54', 'r':'0.55', 'fx':'0.65', 'fy':'0.7',
'gradientUnits':'objectBoundingBox'}, group=doc.defs)
for col, of in (('#fff', 0), ('#e7e7e7', 0.15), ('#ddd', 0.25),
('#aaa', 0.7), ('#888', 0.9), ('#666', 1)):
doc.draw_object('stop', {'offset':of, 'stop-color':col}, group=gradb)
ball_charges = []
for ib in range(2):
ball = doc.draw_object('g', {'id':'metal_ball{:}'.format(ib+1),
'transform':'translate({:.3f},{:.3f})'.format(*([s1, s2][ib]['p'])),
'style':'fill:none; stroke:#000;stroke-linecap:square', 'opacity':1})
# draw rods
if ib == 0:
x1, x2 = -4.1 - s1['p'][0], -0.9 * s1['r']
else:
x1, x2 = 0.9 * s2['r'], 4.1 - s2['p'][0]
doc.draw_object('rect', {'x':x1, 'width':x2-x1,
'y':-0.1/1.2+0.01, 'height':0.2/1.2-0.02,
'style':'fill:url(#rod_shade); stroke-width:0.02'}, group=ball)
# draw metal balls
doc.draw_object('circle', {'cx':0, 'cy':0, 'r':[s1, s2][ib]['r'],
'style':'fill:url(#metal_spot); stroke-width:0.02'}, group=ball)
ball_charges.append(doc.draw_object('g',
{'style':'stroke-width:0.02'}, group=ball))
# find well-distributed start positions of field lines
def get_startpoint_function(startpath, field):
'''
Given a vector function startpath(t), this will return a new
function such that the scalar parameter t in [0,1] progresses
indirectly proportional to the orthogonal field strength.
'''
def dstartpath(t):
return (startpath(t+1e-6) - startpath(t-1e-6)) / 2e-6
def FieldSum(t0, t1):
return ig.quad(lambda t: sc.absolute(sc.cross(
field.F(startpath(t)), dstartpath(t))), t0, t1)[0]
Ftotal = FieldSum(0, 1)
def startpos(s):
t = op.brentq(lambda t: FieldSum(0, t) / Ftotal - s, 0, 1)
return startpath(t)
return startpos
startp = []
def startpath1(t):
phi = 2. * pi * t
return (sc.array(s2['p']) + 1.5 * sc.array([cos(phi), sin(phi)]))
start_func1 = get_startpoint_function(startpath1, field)
nlines1 = 16
for i in range(nlines1):
startp.append(start_func1((0.5 + i) / nlines1))
def startpath2(t):
phi = 2. * pi * (0.195 + 0.61 * t)
return (sc.array(s1['p']) + 1.5 * sc.array([cos(phi), -sin(phi)]))
start_func2 = get_startpoint_function(startpath2, field)
nlines2 = 14
for i in range(nlines2):
startp.append(start_func2((0.5 + i) / nlines2))
# draw the field lines
for p0 in startp:
line = FieldLine(field, p0, directions='both', maxr=7.)
# draw little charge signs near the surface
path_minus = 'M {0:.5f},0 h {1:.5f}'.format(-2./u, 4./u)
path_plus = 'M {0:.5f},0 h {1:.5f} M 0,{0:.5f} v {1:.5f}'.format(-2./u, 4./u)
for si in range(2):
sphere = [s1, s2][si]
# check if fieldline ends inside the sphere
for ci in range(2):
if vabs(line.get_position(ci) - sphere['p']) < sphere['r']:
# find the point where the field line cuts the surface
t = op.brentq(lambda t: vabs(line.get_position(t)
- sphere['p']) - sphere['r'], 0., 1.)
pr = line.get_position(t) - sphere['p']
cpos = 0.9 * sphere['r'] * pr / vabs(pr)
doc.draw_object('path', {'stroke':'black', 'd':
[path_plus, path_minus][ci],
'transform':'translate({:.5f},{:.5f})'.format(
round(u*cpos[0])/u, round(u*cpos[1])/u)},
group=ball_charges[si])
arrow_d = 2.0
of = [0.5 + s1['r'] / arrow_d, 0.5, 0.5, 0.5 + s2['r'] / arrow_d]
doc.draw_line(line, arrows_style={'dist':arrow_d, 'offsets':of})
doc.write()
|
Licensing
[edit]- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 20:05, 30 December 2018 |  | 800 × 600 (46 KB) | Geek3 (talk | contribs) | User created page with UploadWizard |
You cannot overwrite this file.
File usage on Commons
The following 7 pages use this file:
- User talk:Geek3/Archives/2019
- Commons:Quality images/Subject/Non photographic media
- Commons:Quality images candidates/Archives January 03 2019
- File:VFPt metal balls largesmall2 potential+contour.svg
- File:VFPt metal balls largesmall potential+contour.svg
- File:VFPt metal balls largesmall potential.svg
- File:VFPt metal balls largesmall transparent.svg
Metadata
This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.
| Short title | VFPt_metal_balls_largesmall |
|---|---|
| Image title | VFPt_metal_balls_largesmall
created with VectorFieldPlot 1.10 https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot about: https://commons.wikimedia.org/wiki/File:VFPt_metal_balls_largesmall.svg rights: Creative Commons Attribution ShareAlike 4.0 |
| Width | 800 |
| Height | 600 |