File:VFPt metal balls largesmall2 potential+contour.svg

Original file (SVG file, nominally 800 × 600 pixels, file size: 137 KB)
Captions
Captions
Summary
[edit]| DescriptionVFPt metal balls largesmall2 potential+contour.svg |
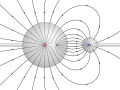
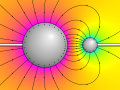
English: Electric field around a large and a small conducting sphere charged with opposite but equal amounts of electric charge. The shape of the field lines is computed exactly, using the method of image charges with an infinite series of charges inside the two spheres. Field lines are always orthogonal to the surface of each sphere. In reality, the field is created by a continuous charge distribution at the surface of each sphere, indicated by small plus and minus signs. The electric potential is depicted as background color with yellow at 0V together with equipotential lines. |
| Date | |
| Source | Own work |
| Author | Geek3 |
| Other versions |
|
| SVG development InfoField | |
| Source code InfoField | Python code# paste this code at the end of VectorFieldPlot 3.1
# https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot
u = 100.0
doc = FieldplotDocument('VFPt_metal_balls_largesmall2_potential+contour',
commons=True, width=800, height=600, unit=u)
# define spheres with position and radius
s1 = {'c':sc.array([-1.0, 0.]), 'r':1.5}
s2 = {'c':sc.array([2.0, 0.]), 'r':0.5}
spheres = [s1, s2]
def U_sphere(sphere, charges):
f = Field([ ['monopole', {'x':c['p'][0], 'y':c['p'][1], 'Q':c['Q']}] for c in charges])
return sc.mean([f.V(sphere['c'] + sphere['r'] * array((cos(phi), sin(phi))))
for phi in sc.linspace(0, 2*pi, 64, endpoint=False)])
def Q_sphere(isphere, charges):
return sum([c['Q'] for c in charges if c['i'] == isphere])
# compute series of charges https://dx.doi.org/10.2174/1874183500902010032
def mirrored_charges(p, Q, isphere, spheres, Qmin):
'''
Recursive function. Returns list of mirrored charges for n spheres
'''
if fabs(Q) < Qmin:
return []
charges = [{'p':p, 'Q':Q, 'i':isphere}]
for i, s in enumerate(spheres):
if i != isphere:
pnew = s['c'] + (p - s['c']) * (s['r'] / vabs(p - s['c']))**2
Qnew = -Q * s['r'] / vabs(p - s['c'])
charges += mirrored_charges(pnew, Qnew, i, spheres, Qmin)
return charges
charges_raw = [mirrored_charges(s['c'], 1., si, spheres, 1e-4) for si,s in enumerate(spheres)]
# Use charge normalization from paper above
# Here one can also solve for charge conditions such as neutrality
matrixU = [ [U_sphere(s, cs) for cs in charges_raw] for s in spheres]
matrixQ = [ [Q_sphere(si, cs) for cs in charges_raw] for si in range(len(spheres))]
Q0, Q1 = 1., -1
charge_factors = sc.linalg.solve(matrixQ, [Q0, Q1])
for il in range(len(charges_raw)):
for ic in range(len(charges_raw[il])):
charges_raw[il][ic]['Q'] *= charge_factors[il]
charges = [c for cl in charges_raw for c in cl]
charges = sorted(charges, key=lambda x: -fabs(x['Q']))
for si, s in enumerate(spheres):
s['U'] = U_sphere(s, charges)
s['Q'] = Q_sphere(si, charges)
#print('sphere', si, s, 'U =', s['U'], 'Q =', s['Q'])
print('using', len(charges), 'mirror charges.')
field = Field([ ['monopole', {'x':c['p'][0], 'y':c['p'][1], 'Q':c['Q']}] for c in charges])
def pot(xy):
for s in spheres:
if vabs(xy - s['c']) <= s['r']:
return s['U']
return field.V(xy)
U0 = max([fabs(U_sphere(s, charges)) for s in spheres])
doc.draw_scalar_field(func=pot, cmap=doc.cmap_AqYlFs, vmin=-U0, vmax=U0)
doc.draw_contours(func=pot, linewidth=1, linecolor='#444444',
levels=sc.linspace(-U0, U0, 25)[1:-1])
# draw symbols
#for c in charges:
# doc.draw_charges(Field([ ['monopole', {'x':c[0][0], 'y':c[0][1], 'Q':c[1]}] ]),
# scale=0.6*sqrt(fabs(c[1])))
gradb = doc.draw_object('radialGradient', {'id':'metal_spot', 'cx':'0.53',
'cy':'0.54', 'r':'0.55', 'fx':'0.65', 'fy':'0.7',
'gradientUnits':'objectBoundingBox'}, group=doc.defs)
for col, of in (('#fff', 0), ('#e7e7e7', 0.15), ('#ddd', 0.25),
('#aaa', 0.7), ('#888', 0.9), ('#666', 1)):
doc.draw_object('stop', {'offset':of, 'stop-color':col}, group=gradb)
ball_charges = []
for ib, s in enumerate(spheres):
ball = doc.draw_object('g', {'id':'metal_ball{:}'.format(ib+1),
'transform':'translate({:.3f},{:.3f})'.format(*(s['c'])),
'style':'fill:none; stroke:#000;stroke-linecap:square', 'opacity':1})
# draw metal balls
doc.draw_object('circle', {'cx':0, 'cy':0, 'r':s['r'],
'style':'fill:url(#metal_spot); stroke-width:0.02'}, group=ball)
ball_charges.append(doc.draw_object('g',
{'style':'stroke-width:0.02'}, group=ball))
def startpath(t):
phi = 2. * pi * t
return s2['c'] + 1.5 * array([cos(phi), sin(phi)])
nlines1 = 22
startpoints = Startpath(field, startpath).npoints(nlines1)
for ip, p0 in enumerate(startpoints):
line = FieldLine(field, p0, directions='both', maxr=1000,
bounds_func=lambda xy: max([s['r'] - vabs(xy-s['c']) for s in [s1, s2]]))
# draw little charge signs near the surface
path_minus = 'M {0:.5f},0 h {1:.5f}'.format(-2./u, 4./u)
path_plus = 'M {0:.5f},0 h {1:.5f} M 0,{0:.5f} v {1:.5f}'.format(-2./u, 4./u)
for si in range(2):
sphere = [s1, s2][si]
# check if fieldline ends inside the sphere
for ci in range(2):
if (vabs(line.get_position(ci) - sphere['c']) < sphere['r'] and
vabs(line.get_position(1-ci) - sphere['c']) > sphere['r']):
# find the point where the field line cuts the surface
t = optimize.brentq(lambda t: vabs(line.get_position(t)
- sphere['c']) - sphere['r'], 0., 1.)
pr = line.get_position(t) - sphere['c']
cpos = (-0.06 + 0.96 * sphere['r']) * vnorm(pr)
doc.draw_object('path', {'stroke':'black', 'd':
[path_plus, path_minus][ci],
'transform':'translate({:.5f},{:.5f})'.format(
round(u*cpos[0])/u, round(u*cpos[1])/u)},
group=ball_charges[si])
ar_st = {'potential':pot, 'at_potentials':[-0.21*U0, 0.1*U0]}
ar_st['scale'] = 1.2
doc.draw_line(line, arrows_style=ar_st)
doc.write()
|
Licensing
[edit]- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 13:09, 30 May 2020 |  | 800 × 600 (137 KB) | Geek3 (talk | contribs) | Uploaded own work with UploadWizard |
You cannot overwrite this file.
File usage on Commons
The following page uses this file:
Metadata
This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.
| Short title | VFPt_metal_balls_largesmall2_potential+contour |
|---|---|
| Image title | VFPt_metal_balls_largesmall2_potential+contour
created with VectorFieldPlot 3.1 https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot about: https://commons.wikimedia.org/wiki/File:VFPt_metal_balls_largesmall2_potential+contour.svg rights: Creative Commons Attribution ShareAlike 4.0 |
| Width | 800 |
| Height | 600 |